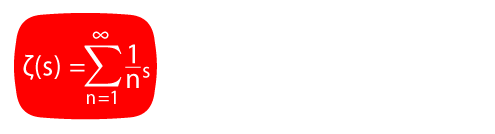Video Content by Date
Speaker: Jin-Cheng Guu
This presentation will introduce a strategy to simplify certain undecidable problems. We will then demonstrate how quantum physics has been utilized to tackle potentially undecidable problems, specifically within the realm of low-dimensional topology. This intersection is known as quantum topology, a field in which I have been actively working, and should time allow, I will present some of my recent results in this area.
Speaker: Felix Christian Clemen
A classical problem in combinatorial geometry, posed by Erdös in 1946, asks to determine the maximum number of unit segments in a set of n points in the plane. Since then a great variety of extremal problems in finite point sets have been studied. Here, we look at generalizations of this question concerning regular simplices. Among others we answer the following question asked by Erdös: Given n points in R6, how many triangles can be equilateral triangles? For our proofs we use hypergraph Turán theory. This is joint work with Dumitrescu and Liu.
Speaker: Michael Lamoureux
As an academic mathematician with a few decades of experience working with industry, the speaker has encountered many challenging problems that required the knowledge and development of a diverse collection of mathematical tools to effectively meet these challenges. This talk will present the mathematics arising in these collaborations, discussing both some technical details and why these skills might be useful to you as a young mathematician interested in an industrial career.
The talk will include work in the oil and gas sector (mathematics of imaging, partial differential equations, inverse problems, numerical methods), psychology and acoustics (Fourier transforms, digital signal processing), smart buildings (mathematical modeling and data science) and K-12 math education (mathematical visualizations and more data science).
There will be a few videos and animations to lighten up the gory technical details!
Speaker: Antoine Leudière
Drinfeld modules are the analogues of elliptic curves in positive characteristic. They are essential objects in number theory for studying function fields. They do not have points, in the traditional sense—we're going to count them anyway! The first methods achieving this were inspired by classical elliptic curve results; we will instead explore an algorithm based on so-called Anderson motives that achieves greater generality. Joint work with Xavier Caruso.
Speaker: Maria Chudnovsky
How does one describe the structure of a graph? What is a good way to measure how complicated a given graph is? Tree decompositions are a powerful tool in structural graph theory, designed to address these questions. To obtain a tree decomposition of a graph G, we break G into parts that interact with each other in a simple ("tree-like") manner. But what properties do the parts need to have in order for the decomposition to be meaningful? Traditionally a parameter called the "width" of a decomposition was considered, that is simply the maximum size of a part. In recent years other ways of measuring the complexity of tree decompositions have been proposed, and their properties are being studied. In this talk we will discuss recent progress in this area, touching on the classical notion of bounded tree-width, concepts of more structural flavor, and the interactions between them.
Speaker: Antoine Leudière
In number theory, we often consider a generalization of integers called algebraic numbers. Their definition is rather elementary, but their classification is nothing but. Algebraic numbers come in families, and we can attach each family an invariant measuring its size: the castle. Kronecker proved that an algebraic integer with castle strictly less than one is zero, and that an algebraic integer with castle exactly one is a root of unity. The classification of algebraic numbers with castle less than a prescribed constant is technical, but we managed to derive it for cyclotomic integers (a subclass of algebraic numbers) with castle less than 5.01, solving a conjecture of R. M. Robinson opened in 1965.
I will state our result, and rather than focus on the technical details, present the methodology that lead us to it. Indeed, this collaboration was initiated at the Rethinking Number Theory workshop: members from various career stages work in groups under the guidance of a project leader. The workshop organizers make it so that participants work with joy, autonomy and open-mindness. This allowed each of us to contribute to what we were best at. Joint work with J. Bajpai, S. Das, K. S. Kedlaya, N. H. Le, M. Lee and J. Mello; https://arxiv.org/abs/2510.20435.
Speaker: Do Nhat Tan Vo
Fix a positive integer $X$ and multi-sets of complex numbers $\mathcal{I}$ and $\mathcal{J}$. We study the shifted convolution sum \[ D_{\mathcal{I},\mathcal{J}}(X,1) = \sum_{n\leq X} \tau_{\mathcal{I}}(n)\tau_{\mathcal{J}}(n+1), \] where $\tau_{\mathcal{I}}$ and $\tau_{\mathcal{J}}$ are shifted divisor functions. These sums naturally appear in the study of higher moments of the Riemann zeta function and additive problems in number theory. We review known results on $2k$-th moment of the Riemann zeta function and correlation sums associated with generalized divisor function. Assuming a conjectural bound on the averaged level of distribution of $\tau_{\mathcal{J}}(n)$ in arithmetic progressions, we present an asymptotic formula for $D_{\mathcal{I},\mathcal{J}}(X,1)$ with explicit main terms and power-saving error estimates.
Speaker: Tianxia (Tylar) Jia
We use a U-Net to make baseline power forecasts and train a diffusion model on its residuals to capture uncertainty. The diffusion samples naturally show low ensemble spread during stable atmospheric conditions and much wider spread when the atmosphere is more turbulent. This improves both reliability and interpretability compared to using the U-Net alone. The method provides a practical alternative to running full WRF simulations for uncertainty-aware wind farm power modelling.
Speaker: Maya Sankar
I will discuss several recent results on the Turán density of long cycle-like hypergraphs. These results (due to Kamčev–Letzter–Pokrovskiy, Balogh–Luo, and myself) all follow a similar framework, and I will outline a general strategy to prove Turán-type results for tight cycles in larger uniformities or for other "cycle-like" hypergraphs.
One key ingredient in this framework, which I hope to prove in full, is a hypergraph analogue of the statement that a graph has no odd closed walks if and only if it is bipartite. More precisely, for various classes C of "cycle-like" r-uniform hypergraphs — including, for any k, the family of tight cycles of length k modulo r — we equiivalently characterize C-hom-free hypergraphs as those admitting a certain type of coloring of (r-1)-tuples of vertices. This provides a common generalization of results due to Kamčev–Letzter–Pokrovskiy and Balogh–Luo.
Speaker: Brent Pym
A number is called a "period" if it can be expressed as the volume of a region in Euclidean space, defined by polynomial inequalities with rational coefficients. Many famous constants, such as π, log(2) and special values of the Riemann zeta function, are periods. Consequently, periods play an important role in many parts of mathematics and science. For example, they arise naturally when relating the mathematics of classical and quantum mechanics (Poisson geometry and noncommutative algebra, respectively), via a procedure known as "deformation quantization". It turns out that algebraic geometry endows periods with a wealth of rich and surprising structure, such as a "motivic Galois group" of symmetries, which constrains their properties and facilitates their calculation. I will give an introduction to this circle of ideas, emphasizing their role in recent developments in deformation quantization.
Speaker: Juanita Duque Rosero
Triangular modular curves are a generalization of modular curves and arise as quotients of the complex upper half-plane by congruence subgroups of hyperbolic triangle groups. These curves naturally parameterize hypergeometric abelian varieties, making them interesting arithmetic objects. In this talk, we will focus on the Borel-kind triangular modular curves. We will show that when restricting to prime level, there are finitely many such curves of any given genus, and there is an algorithm to enumerate them. Time permitting, we will explore generalizations to composite level. This is joint work with John Voight.
Speaker: Dylan King
The Turan density of a forbidden hypergraph F is the largest edge density a large hypergraph H can have without containing any copy of F, and determining this number for various F is a notoriously difficult problem. One on-ramp to this question (from Erdos and Sos) is to furthermore require that the hyperedges of H are distributed nearly uniformly across the vertices, giving the uniform Turan density of F. All known examples of such uniformly dense H avoiding some F follow the so-called “palette” construction of Rodl. In this talk we will introduce each of these notions before discussing our main result, that any palette can be obtained as an extremal construction for some finite family of forbidden subgraph F, which will require the tools of hypergraph regularity and Lagrangians. As an application we can obtain some (interesting) new values as the uniform Turan density of forbidden families.
Based on joint work with Simon Piga, Marcelo Sales, and Bjarne Schuelke.
Speaker: Annie Innes-Gold
‘Reef halos’ are rings of sand, barren of vegetation, encircling reefs. However, the extent to which various biotic (e.g., herbivory) and abiotic (e.g., temperature, nutrients) factors drive changes in halo prevalence and size remains unclear. The objective of this study was to explore the effects of herbivore biomass, primary productivity, temperature, and nutrients on reef halo presence and width. First, we conducted a field study using artificial reef structures and their surrounding halos, finding that halos were more likely to be observed with high herbivorous fish biomass, and halos were larger under high temperatures. There was a distinct interaction between herbivorous fish biomass and temperature, where at high fish biomass, halos were more likely to be observed under low temperatures. Second, we incorporated environmental drivers into a consumer-resource model of halo dynamics. Certain formulations of temperature-dependent vegetation growth caused halo width and fish density to change from a fixed to an oscillating system, supporting the idea that environmental drivers can cause temporal fluctuations in halo width. Our unique combination of field-based and mechanistic modeling approaches has enhanced our understanding of the role of environmental drivers in grazing patterns, which will be particularly important as climate change causes shifts in marine systems worldwide.
Speaker: Behruz Tayfeh-Rezaie
Fix a positive integer $n$ and a graph $F$. A graph $G$ with $n$ vertices is called $F$-saturated if $G$ contains no subgraph isomorphic to $F$ but each graph obtained from $G$ by joining a pair of nonadjacent vertices contains at least one copy of $F$ as a subgraph. The saturation function of $F$, denoted $\mathrm{sat}(n, F)$, is the minimum number of edges in an $F$-saturated graph on $n$ vertices. This parameter along with its counterpart, i.e. Turan number, have been investigated for quite a long time.
We review known results on $\mathrm{sat}(n, F)$ for various graphs $F$. We also present new results when $F$ is a complete multipartite graph or a cycle graph. The problem of saturation in the Erdos-Renyi random graph $G(n, p)$ was introduced by Korandi and Sudakov in 2017. We survey the results for random case and present our latest results on saturation numbers of bipartite graphs in random graphs.
Speaker: Lucas Villagra Torcomian
In this talk we will introduce the modular method, the approach followed by Wiles to prove Fermat’s Last Theorem. We will explain the role of elliptic curves, modular forms, and Galois representations in this framework, and discuss how the method has evolved in recent years.
Speaker: Clinton H. Durney
Mathematical biology offers powerful tools to tackle pressing problems at the interface of health and public policy. In this talk, I will share two vignettes demonstrating how mathematical and simulation modelling can be applied to tobacco regulatory science. The first uses a Markov state transition framework to capture population-level dynamics of two tobacco products, each with a flavour option. This structure highlights the challenges of modelling high-dimensional systems, parameter inference from sparse data, and representing policy interventions as modifications to initiation, cessation, and product switching rates. The second vignette focuses on social network modelling, where adolescent tobacco use is primarily shaped by peer influence and network structure. In this setting, stochastic processes and graph-based models describe how behaviours propagate and stabilise within adolescent populations. Together, these examples illustrate how applied mathematics can bridge data and policy in public health.
Speaker: Caleb Marshall
A vanishing sum of roots of unity (VSRU) is a finite list $z_1,\ldots,z_K$ of $N$-th complex roots of unity whose sum is zero. While there are many simple examples—including the famous "beautiful equation" of Euler, $e^{i \pi} + 1 = 0$—such sums become extremely complex as the parameter $N$ attains more complex prime power divisors (and we will see several classical examples illustrating this idea, as well as new examples from my work).
One fruitful line of inquiry is to seek a quantitative relationship between the prime divisors of $N$, their associated exponents, and the cardinality parameter $K$. A theorem of T.Y. Lam and K.H. Leung from the early '90's states: $K$ must always be (at least) as large as the smallest prime dividing $N$. This generalizes the well known observation that that sum of all $p$-th roots of unity (where $p$ is any prime number) must vanish; and, one notices that Euler's equation is one example of this fact.
In this talk, we will discuss two significant strengthenings of this result (one due to myself and I. Łaba, another due to myself, G. Kiss, I. Łaba and G. Somlai), which are derived from complexity measurements for polynomials with integer coefficients which have many cyclotomic polynomial divisors. As applications, we give connections in two other areas of mathematics. The first is in the study of integer tilings: additive decompositions of the integers $Z = A+B$ as a sum set, where each integer is represented uniquely. The second application is to the Favard length problem in fractal geometry, which asks for bounds upon the average length of the projections of certain dynamically-defined fractals onto lines.
This talk is based upon my individual work, as well as my joint work with I. Łaba, as well as my joint work with G. Kiss, I. Łaba and G. Somlai. All are welcome, and the first 15-20 minutes will include introductory ideas and examples for all results discussed in the latter portion of the talk.
Speaker: John Stockie
Industrial mathematics is a field that spans a broad spectrum of activity ranging from applied R&D performed by mathematicians employed in industry, to purely academic research projects undertaken by university mathematics professors. In this talk, I will survey several research projects I have been involved with that fall under the heading of what I'll call "mathematics *for* industry", which relates specifically to direct collaborations between university mathematicians and non-academic partner organizations. These projects encompass a diverse collection of mathematical techniques (ranging from simple algebra to partial differential equations, finite volume methods, inverse problems and homogenization theory) as well as applications from many scientific disciplines (such as fluid mechanics, image processing, atmospheric science and plant biology). In the process, I will attempt to characterize the job of an industrial mathematician and to identify the qualities and skills that are most desirable for anyone interested in making significant contributions to research at the interface between university and industry. I also hope to convince you that industrial collaborations can be a rich source of challenging and novel mathematical problems for academic mathematicians.
Speaker: Niall Taggart
There is a striking and useful analogy between equivariant homotopy theory and functor calculus. In the equivariant setting, Greenlees conjectured that the category of rational G-spectra has an algebraic model - meaning it is equivalent to the derived category of an abelian category with desirable finiteness properties. This talk will examine the functor calculus counterpart of this conjecture in (potentially) more than one flavour of functor calculus. (Joint work with D. Barnes and M. Kedziorek.)
Speaker: Curtis McMullen
In this talk, titled "The Question Mark Function, Welding, and Complex Dynamics," Prof. McMullen will explore a fascinating interplay of ideas drawn from number theory, conformal geometry, and dynamical systems. While the abstract remains intentionally open-ended, the colloquium promises a thought-provoking look at mathematical structures that defy easy categorization.
Speaker: JC Loredo-Osti
The many ways to model an infectious disease go from simple predator-prey Lotka-Volterra compartmentalised models to highly dimensional models. These models are also commonly expressed as the solution to a system of deterministic differential equations. One issue with models that are highly parametrised, which makes them unsuitable for the early stages of an outbreak, is that estimation with a few data points may be impractical. In terms of sampling, small populations are peculiar, e.g., one may find very effective contact tracing along quite noisy data collection and management due to the lack of resources, and a scarcity of methodological developments crafted for those populations. In this presentation, I will argue that in small jurisdictions, stochastic branching and self-exciting processes or variations of basic compartmentalised models are more relevant because of the volatile nature of the disease dynamics, particularly at early stages of an outbreak. Then, we will focus on continuous-time Markov chain compartmentalised models and their parameter estimation through the likelihood. Finally, we comment on the connection of SIR-like models with Hawkes processes. For those unable to attend in person, you can join via Zoom using the link below.
Speaker: Abbas Maarefparvar
In this talk, we first introduce the Brumer-Rosen-Zantema exact sequence (BRZ), a four-term sequence related to strongly ambiguous ideal classes in finite Galois extensions of number fields. Then, using BRZ, we obtain some known cohomological results in the literature concerning Hilbert's Theorem 94, the capitulation map, and the Principal Ideal Theorem. This is a joint work with Ali Rajaei (Tarbiat Modares University) and Ehsan Shahoseini (Institute for Research in Fundamental Sciences).
Speaker: Alex Beams
Phylogenetic trees are mathematical objects that encode information about ancestry relationships and are often used in the interpretation of genomic data. They have proved especially useful for advancing our understanding of pathogen populations that evolve on observable timescales, and the construction of phylogenies and our interpretations of them rely on mathematical models at every step. In this talk, we will discuss ongoing projects that focus on the bacterium that causes Tuberculosis. In the first project, we connect compartmental models of disease transmission to pathogen phylogenies in order to understand how epidemiological processes affect tree shape. In the second project, we aim to reconstruct movement patterns on phylogenies to inform the likely efficacy of geographically-targeted public health interventions. In both of these projects, mathematical models play an essential role in the interpretation of phylogenies, and that seems likely to be the case for any statistical inferences we hope to draw from genomic data for the foreseeable future.
Speaker: Cindy Greenwood
The rainbow and the brain have in common that frequencies are produced. In both cases there is a function of frequency, f, called the power spectral density (PSD). In both cases invasive investigation spoils the investigated object. This talk will describe using noninvasive electroencephalography (EEG) to evaluate the PSD of the brain, via stochastic modelling of associated brain structure. We explore the popular question: does the human brain manifest the mysterious property called "1/f"? Is the PSD of the brain proportional to the function "f to the power -a", for some a > 0, and hence scale-free? What would that mean about the brain? Independent of these fascinating questions, the exponent, a, has many successful applications as a diagnostic of brain disorders and treatments.
Speaker: Nathanael Berestycki
I will discuss Liouville Brownian motion, the canonical diffusion in the random geometry defined by Liouville quantum gravity (LQG). In particular I will present some recent results on the spectral geometry of LQG, showing that the eigenvalues satisfy a Weyl law. We will also discuss a number of striking conjectures which aim to relate LQG to a phenomenon known as "quantum chaos", which will also be explained.
Speaker: Mathav Murugan
The heat kernel is the fundamental solution to a parabolic partial differential equation. From a probabilistic perspective, the heat kernel is the transition probability density of a stochastic process. Harnack inequalities and functional inequalities such as Poincare and Sobolev inequalities provide tools to understand the relationship between the behavior of the heat kernel and the geometry of the underlying space. An important feature of the approach using functional inequalities is its robustness under perturbations.
The study of the heat kernel and its estimates has produced fruitful interactions between the fields of Analysis, Geometry, and Probability. One of the goals of this course is to illustrate these interactions of heat kernel estimates with functional inequalities, boundary trace processes, quasisymmetric maps, circle packings, the time change of Markov processes, Doob's h-transform, and estimates of harmonic measure or exit distribution.
The setting for this course is a symmetric Markov process which is equivalentlydescribed using a Dirichlet form. This course will contain an introduction to the theory of Dirichlet forms. This theory will be used to construct and analyze Markov processes. This course will survey both classical results and recent progress in our understanding of heat kernel estimates and Harnack inequalities.
Speaker: Tom Hutchcroft
In Bernoulli bond percolation, we delete or retain each edge of a graph independently at random with some retention parameter p and study the geometry of the connected components (clusters) of the resulting subgraph. For lattices of dimension d>1, percolation has a phase transition, with a infinite cluster emerging at a critical probability pc(d). It is believed that critical percolation at and near the critical probability exhibits rich, fractal-like geometry that is expected to be approximately independent of the choice of lattice but highly dependent on the dimension d. In particular, various qualitative distinctions are expected between the low dimensional case d<6, the high-dimensional case d>6, and the critical case d=6, but this remains poorly understood particularly in dimensions d=3,4,5,6.
In this course, I will give an overview of of what is known about critical percolation, focussing on the non-planar models and including a detailed treatment of recent advances in long-range and hierarchical models for which various aspects of intermediate-dimensional critical phenomena can now be understood rigorously.
No prior knowledge of percolation will be assumed.
Speaker: Nathanael Berestycki
I will discuss Liouville Brownian motion, the canonical diffusion in the random geometry defined by Liouville quantum gravity (LQG). In particular I will present some recent results on the spectral geometry of LQG, showing that the eigenvalues satisfy a Weyl law. We will also discuss a number of striking conjectures which aim to relate LQG to a phenomenon known as "quantum chaos", which will also be explained.
Speaker: Tom Hutchcroft
In Bernoulli bond percolation, we delete or retain each edge of a graph independently at random with some retention parameter p and study the geometry of the connected components (clusters) of the resulting subgraph. For lattices of dimension d>1, percolation has a phase transition, with a infinite cluster emerging at a critical probability pc(d). It is believed that critical percolation at and near the critical probability exhibits rich, fractal-like geometry that is expected to be approximately independent of the choice of lattice but highly dependent on the dimension d. In particular, various qualitative distinctions are expected between the low dimensional case d<6, the high-dimensional case d>6, and the critical case d=6, but this remains poorly understood particularly in dimensions d=3,4,5,6.
In this course, I will give an overview of of what is known about critical percolation, focussing on the non-planar models and including a detailed treatment of recent advances in long-range and hierarchical models for which various aspects of intermediate-dimensional critical phenomena can now be understood rigorously.
No prior knowledge of percolation will be assumed.
Speaker: Mathav Murugan
The heat kernel is the fundamental solution to a parabolic partial differential equation. From a probabilistic perspective, the heat kernel is the transition probability density of a stochastic process. Harnack inequalities and functional inequalities such as Poincare and Sobolev inequalities provide tools to understand the relationship between the behavior of the heat kernel and the geometry of the underlying space. An important feature of the approach using functional inequalities is its robustness under perturbations.
The study of the heat kernel and its estimates has produced fruitful interactions between the fields of Analysis, Geometry, and Probability. One of the goals of this course is to illustrate these interactions of heat kernel estimates with functional inequalities, boundary trace processes, quasisymmetric maps, circle packings, the time change of Markov processes, Doob's h-transform, and estimates of harmonic measure or exit distribution.
The setting for this course is a symmetric Markov process which is equivalentlydescribed using a Dirichlet form. This course will contain an introduction to the theory of Dirichlet forms. This theory will be used to construct and analyze Markov processes. This course will survey both classical results and recent progress in our understanding of heat kernel estimates and Harnack inequalities.
Speaker: Nathanael Berestycki
I will discuss Liouville Brownian motion, the canonical diffusion in the random geometry defined by Liouville quantum gravity (LQG). In particular I will present some recent results on the spectral geometry of LQG, showing that the eigenvalues satisfy a Weyl law. We will also discuss a number of striking conjectures which aim to relate LQG to a phenomenon known as "quantum chaos", which will also be explained.
Speaker: Mathav Murugan
The heat kernel is the fundamental solution to a parabolic partial differential equation. From a probabilistic perspective, the heat kernel is the transition probability density of a stochastic process. Harnack inequalities and functional inequalities such as Poincare and Sobolev inequalities provide tools to understand the relationship between the behavior of the heat kernel and the geometry of the underlying space. An important feature of the approach using functional inequalities is its robustness under perturbations.
The study of the heat kernel and its estimates has produced fruitful interactions between the fields of Analysis, Geometry, and Probability. One of the goals of this course is to illustrate these interactions of heat kernel estimates with functional inequalities, boundary trace processes, quasisymmetric maps, circle packings, the time change of Markov processes, Doob's h-transform, and estimates of harmonic measure or exit distribution.
The setting for this course is a symmetric Markov process which is equivalentlydescribed using a Dirichlet form. This course will contain an introduction to the theory of Dirichlet forms. This theory will be used to construct and analyze Markov processes. This course will survey both classical results and recent progress in our understanding of heat kernel estimates and Harnack inequalities.
Speaker: Tom Hutchcroft
In Bernoulli bond percolation, we delete or retain each edge of a graph independently at random with some retention parameter p and study the geometry of the connected components (clusters) of the resulting subgraph. For lattices of dimension d>1, percolation has a phase transition, with a infinite cluster emerging at a critical probability pc(d). It is believed that critical percolation at and near the critical probability exhibits rich, fractal-like geometry that is expected to be approximately independent of the choice of lattice but highly dependent on the dimension d. In particular, various qualitative distinctions are expected between the low dimensional case d<6, the high-dimensional case d>6, and the critical case d=6, but this remains poorly understood particularly in dimensions d=3,4,5,6.
In this course, I will give an overview of of what is known about critical percolation, focussing on the non-planar models and including a detailed treatment of recent advances in long-range and hierarchical models for which various aspects of intermediate-dimensional critical phenomena can now be understood rigorously.
No prior knowledge of percolation will be assumed.
Speaker: Tom Hutchcroft
In Bernoulli bond percolation, we delete or retain each edge of a graph independently at random with some retention parameter p and study the geometry of the connected components (clusters) of the resulting subgraph. For lattices of dimension d>1, percolation has a phase transition, with a infinite cluster emerging at a critical probability pc(d). It is believed that critical percolation at and near the critical probability exhibits rich, fractal-like geometry that is expected to be approximately independent of the choice of lattice but highly dependent on the dimension d. In particular, various qualitative distinctions are expected between the low dimensional case d<6, the high-dimensional case d>6, and the critical case d=6, but this remains poorly understood particularly in dimensions d=3,4,5,6.
In this course, I will give an overview of of what is known about critical percolation, focussing on the non-planar models and including a detailed treatment of recent advances in long-range and hierarchical models for which various aspects of intermediate-dimensional critical phenomena can now be understood rigorously.
No prior knowledge of percolation will be assumed.
Speaker: Mathav Murugan
The heat kernel is the fundamental solution to a parabolic partial differential equation. From a probabilistic perspective, the heat kernel is the transition probability density of a stochastic process. Harnack inequalities and functional inequalities such as Poincare and Sobolev inequalities provide tools to understand the relationship between the behavior of the heat kernel and the geometry of the underlying space. An important feature of the approach using functional inequalities is its robustness under perturbations.
The study of the heat kernel and its estimates has produced fruitful interactions between the fields of Analysis, Geometry, and Probability. One of the goals of this course is to illustrate these interactions of heat kernel estimates with functional inequalities, boundary trace processes, quasisymmetric maps, circle packings, the time change of Markov processes, Doob's h-transform, and estimates of harmonic measure or exit distribution.
The setting for this course is a symmetric Markov process which is equivalentlydescribed using a Dirichlet form. This course will contain an introduction to the theory of Dirichlet forms. This theory will be used to construct and analyze Markov processes. This course will survey both classical results and recent progress in our understanding of heat kernel estimates and Harnack inequalities.
Speaker: Mathav Murugan
The heat kernel is the fundamental solution to a parabolic partial differential equation. From a probabilistic perspective, the heat kernel is the transition probability density of a stochastic process. Harnack inequalities and functional inequalities such as Poincare and Sobolev inequalities provide tools to understand the relationship between the behavior of the heat kernel and the geometry of the underlying space. An important feature of the approach using functional inequalities is its robustness under perturbations.
The study of the heat kernel and its estimates has produced fruitful interactions between the fields of Analysis, Geometry, and Probability. One of the goals of this course is to illustrate these interactions of heat kernel estimates with functional inequalities, boundary trace processes, quasisymmetric maps, circle packings, the time change of Markov processes, Doob's h-transform, and estimates of harmonic measure or exit distribution.
The setting for this course is a symmetric Markov process which is equivalentlydescribed using a Dirichlet form. This course will contain an introduction to the theory of Dirichlet forms. This theory will be used to construct and analyze Markov processes. This course will survey both classical results and recent progress in our understanding of heat kernel estimates and Harnack inequalities.
Speaker: Tom Hutchcroft
In Bernoulli bond percolation, we delete or retain each edge of a graph independently at random with some retention parameter p and study the geometry of the connected components (clusters) of the resulting subgraph. For lattices of dimension d>1, percolation has a phase transition, with a infinite cluster emerging at a critical probability pc(d). It is believed that critical percolation at and near the critical probability exhibits rich, fractal-like geometry that is expected to be approximately independent of the choice of lattice but highly dependent on the dimension d. In particular, various qualitative distinctions are expected between the low dimensional case d<6, the high-dimensional case d>6, and the critical case d=6, but this remains poorly understood particularly in dimensions d=3,4,5,6.
In this course, I will give an overview of of what is known about critical percolation, focussing on the non-planar models and including a detailed treatment of recent advances in long-range and hierarchical models for which various aspects of intermediate-dimensional critical phenomena can now be understood rigorously.
No prior knowledge of percolation will be assumed.
Speaker: Tom Hutchcroft
In Bernoulli bond percolation, we delete or retain each edge of a graph independently at random with some retention parameter p and study the geometry of the connected components (clusters) of the resulting subgraph. For lattices of dimension d>1, percolation has a phase transition, with a infinite cluster emerging at a critical probability pc(d). It is believed that critical percolation at and near the critical probability exhibits rich, fractal-like geometry that is expected to be approximately independent of the choice of lattice but highly dependent on the dimension d. In particular, various qualitative distinctions are expected between the low dimensional case d<6, the high-dimensional case d>6, and the critical case d=6, but this remains poorly understood particularly in dimensions d=3,4,5,6.
In this course, I will give an overview of of what is known about critical percolation, focussing on the non-planar models and including a detailed treatment of recent advances in long-range and hierarchical models for which various aspects of intermediate-dimensional critical phenomena can now be understood rigorously.
No prior knowledge of percolation will be assumed.
Speaker: Mathav Murugan
The heat kernel is the fundamental solution to a parabolic partial differential equation. From a probabilistic perspective, the heat kernel is the transition probability density of a stochastic process. Harnack inequalities and functional inequalities such as Poincare and Sobolev inequalities provide tools to understand the relationship between the behavior of the heat kernel and the geometry of the underlying space. An important feature of the approach using functional inequalities is its robustness under perturbations.
The study of the heat kernel and its estimates has produced fruitful interactions between the fields of Analysis, Geometry, and Probability. One of the goals of this course is to illustrate these interactions of heat kernel estimates with functional inequalities, boundary trace processes, quasisymmetric maps, circle packings, the time change of Markov processes, Doob's h-transform, and estimates of harmonic measure or exit distribution.
The setting for this course is a symmetric Markov process which is equivalentlydescribed using a Dirichlet form. This course will contain an introduction to the theory of Dirichlet forms. This theory will be used to construct and analyze Markov processes. This course will survey both classical results and recent progress in our understanding of heat kernel estimates and Harnack inequalities.
Speaker: Mathav Murugan
The heat kernel is the fundamental solution to a parabolic partial differential equation. From a probabilistic perspective, the heat kernel is the transition probability density of a stochastic process. Harnack inequalities and functional inequalities such as Poincare and Sobolev inequalities provide tools to understand the relationship between the behavior of the heat kernel and the geometry of the underlying space. An important feature of the approach using functional inequalities is its robustness under perturbations.
The study of the heat kernel and its estimates has produced fruitful interactions between the fields of Analysis, Geometry, and Probability. One of the goals of this course is to illustrate these interactions of heat kernel estimates with functional inequalities, boundary trace processes, quasisymmetric maps, circle packings, the time change of Markov processes, Doob's h-transform, and estimates of harmonic measure or exit distribution.
The setting for this course is a symmetric Markov process which is equivalentlydescribed using a Dirichlet form. This course will contain an introduction to the theory of Dirichlet forms. This theory will be used to construct and analyze Markov processes. This course will survey both classical results and recent progress in our understanding of heat kernel estimates and Harnack inequalities.
Speaker: Tom Hutchcroft
In Bernoulli bond percolation, we delete or retain each edge of a graph independently at random with some retention parameter p and study the geometry of the connected components (clusters) of the resulting subgraph. For lattices of dimension d>1, percolation has a phase transition, with a infinite cluster emerging at a critical probability pc(d). It is believed that critical percolation at and near the critical probability exhibits rich, fractal-like geometry that is expected to be approximately independent of the choice of lattice but highly dependent on the dimension d. In particular, various qualitative distinctions are expected between the low dimensional case d<6, the high-dimensional case d>6, and the critical case d=6, but this remains poorly understood particularly in dimensions d=3,4,5,6.
In this course, I will give an overview of of what is known about critical percolation, focussing on the non-planar models and including a detailed treatment of recent advances in long-range and hierarchical models for which various aspects of intermediate-dimensional critical phenomena can now be understood rigorously.
No prior knowledge of percolation will be assumed.
Speaker: Tom Hutchcroft
In Bernoulli bond percolation, we delete or retain each edge of a graph independently at random with some retention parameter p and study the geometry of the connected components (clusters) of the resulting subgraph. For lattices of dimension d>1, percolation has a phase transition, with a infinite cluster emerging at a critical probability pc(d). It is believed that critical percolation at and near the critical probability exhibits rich, fractal-like geometry that is expected to be approximately independent of the choice of lattice but highly dependent on the dimension d. In particular, various qualitative distinctions are expected between the low dimensional case d<6, the high-dimensional case d>6, and the critical case d=6, but this remains poorly understood particularly in dimensions d=3,4,5,6.
In this course, I will give an overview of of what is known about critical percolation, focussing on the non-planar models and including a detailed treatment of recent advances in long-range and hierarchical models for which various aspects of intermediate-dimensional critical phenomena can now be understood rigorously.
No prior knowledge of percolation will be assumed.
Speaker: Mathav Murugan
The heat kernel is the fundamental solution to a parabolic partial differential equation. From a probabilistic perspective, the heat kernel is the transition probability density of a stochastic process. Harnack inequalities and functional inequalities such as Poincare and Sobolev inequalities provide tools to understand the relationship between the behavior of the heat kernel and the geometry of the underlying space. An important feature of the approach using functional inequalities is its robustness under perturbations.
The study of the heat kernel and its estimates has produced fruitful interactions between the fields of Analysis, Geometry, and Probability. One of the goals of this course is to illustrate these interactions of heat kernel estimates with functional inequalities, boundary trace processes, quasisymmetric maps, circle packings, the time change of Markov processes, Doob's h-transform, and estimates of harmonic measure or exit distribution.
The setting for this course is a symmetric Markov process which is equivalentlydescribed using a Dirichlet form. This course will contain an introduction to the theory of Dirichlet forms. This theory will be used to construct and analyze Markov processes. This course will survey both classical results and recent progress in our understanding of heat kernel estimates and Harnack inequalities.
Speaker: Mathav Murugan
The heat kernel is the fundamental solution to a parabolic partial differential equation. From a probabilistic perspective, the heat kernel is the transition probability density of a stochastic process. Harnack inequalities and functional inequalities such as Poincare and Sobolev inequalities provide tools to understand the relationship between the behavior of the heat kernel and the geometry of the underlying space. An important feature of the approach using functional inequalities is its robustness under perturbations.
The study of the heat kernel and its estimates has produced fruitful interactions between the fields of Analysis, Geometry, and Probability. One of the goals of this course is to illustrate these interactions of heat kernel estimates with functional inequalities, boundary trace processes, quasisymmetric maps, circle packings, the time change of Markov processes, Doob's h-transform, and estimates of harmonic measure or exit distribution.
The setting for this course is a symmetric Markov process which is equivalentlydescribed using a Dirichlet form. This course will contain an introduction to the theory of Dirichlet forms. This theory will be used to construct and analyze Markov processes. This course will survey both classical results and recent progress in our understanding of heat kernel estimates and Harnack inequalities.
Speaker: Tom Hutchcroft
In Bernoulli bond percolation, we delete or retain each edge of a graph independently at random with some retention parameter p and study the geometry of the connected components (clusters) of the resulting subgraph. For lattices of dimension d>1, percolation has a phase transition, with a infinite cluster emerging at a critical probability pc(d). It is believed that critical percolation at and near the critical probability exhibits rich, fractal-like geometry that is expected to be approximately independent of the choice of lattice but highly dependent on the dimension d. In particular, various qualitative distinctions are expected between the low dimensional case d<6, the high-dimensional case d>6, and the critical case d=6, but this remains poorly understood particularly in dimensions d=3,4,5,6.
In this course, I will give an overview of of what is known about critical percolation, focussing on the non-planar models and including a detailed treatment of recent advances in long-range and hierarchical models for which various aspects of intermediate-dimensional critical phenomena can now be understood rigorously.
No prior knowledge of percolation will be assumed.
Speaker: Tom Hutchcroft
In Bernoulli bond percolation, we delete or retain each edge of a graph independently at random with some retention parameter p and study the geometry of the connected components (clusters) of the resulting subgraph. For lattices of dimension d>1, percolation has a phase transition, with a infinite cluster emerging at a critical probability pc(d). It is believed that critical percolation at and near the critical probability exhibits rich, fractal-like geometry that is expected to be approximately independent of the choice of lattice but highly dependent on the dimension d. In particular, various qualitative distinctions are expected between the low dimensional case d<6, the high-dimensional case d>6, and the critical case d=6, but this remains poorly understood particularly in dimensions d=3,4,5,6.
In this course, I will give an overview of of what is known about critical percolation, focussing on the non-planar models and including a detailed treatment of recent advances in long-range and hierarchical models for which various aspects of intermediate-dimensional critical phenomena can now be understood rigorously.
No prior knowledge of percolation will be assumed.
Speaker: Mathav Murugan
The heat kernel is the fundamental solution to a parabolic partial differential equation. From a probabilistic perspective, the heat kernel is the transition probability density of a stochastic process. Harnack inequalities and functional inequalities such as Poincare and Sobolev inequalities provide tools to understand the relationship between the behavior of the heat kernel and the geometry of the underlying space. An important feature of the approach using functional inequalities is its robustness under perturbations.
The study of the heat kernel and its estimates has produced fruitful interactions between the fields of Analysis, Geometry, and Probability. One of the goals of this course is to illustrate these interactions of heat kernel estimates with functional inequalities, boundary trace processes, quasisymmetric maps, circle packings, the time change of Markov processes, Doob's h-transform, and estimates of harmonic measure or exit distribution.
The setting for this course is a symmetric Markov process which is equivalentlydescribed using a Dirichlet form. This course will contain an introduction to the theory of Dirichlet forms. This theory will be used to construct and analyze Markov processes. This course will survey both classical results and recent progress in our understanding of heat kernel estimates and Harnack inequalities.
Speaker: Mathav Murugan
The heat kernel is the fundamental solution to a parabolic partial differential equation. From a probabilistic perspective, the heat kernel is the transition probability density of a stochastic process. Harnack inequalities and functional inequalities such as Poincare and Sobolev inequalities provide tools to understand the relationship between the behavior of the heat kernel and the geometry of the underlying space. An important feature of the approach using functional inequalities is its robustness under perturbations.
The study of the heat kernel and its estimates has produced fruitful interactions between the fields of Analysis, Geometry, and Probability. One of the goals of this course is to illustrate these interactions of heat kernel estimates with functional inequalities, boundary trace processes, quasisymmetric maps, circle packings, the time change of Markov processes, Doob's h-transform, and estimates of harmonic measure or exit distribution.
The setting for this course is a symmetric Markov process which is equivalentlydescribed using a Dirichlet form. This course will contain an introduction to the theory of Dirichlet forms. This theory will be used to construct and analyze Markov processes. This course will survey both classical results and recent progress in our understanding of heat kernel estimates and Harnack inequalities.
Speaker: Tom Hutchcroft
In Bernoulli bond percolation, we delete or retain each edge of a graph independently at random with some retention parameter p and study the geometry of the connected components (clusters) of the resulting subgraph. For lattices of dimension d>1, percolation has a phase transition, with a infinite cluster emerging at a critical probability pc(d). It is believed that critical percolation at and near the critical probability exhibits rich, fractal-like geometry that is expected to be approximately independent of the choice of lattice but highly dependent on the dimension d. In particular, various qualitative distinctions are expected between the low dimensional case d<6, the high-dimensional case d>6, and the critical case d=6, but this remains poorly understood particularly in dimensions d=3,4,5,6.
In this course, I will give an overview of of what is known about critical percolation, focussing on the non-planar models and including a detailed treatment of recent advances in long-range and hierarchical models for which various aspects of intermediate-dimensional critical phenomena can now be understood rigorously.
No prior knowledge of percolation will be assumed.
Speaker: Tom Hutchcroft
In Bernoulli bond percolation, we delete or retain each edge of a graph independently at random with some retention parameter p and study the geometry of the connected components (clusters) of the resulting subgraph. For lattices of dimension d>1, percolation has a phase transition, with a infinite cluster emerging at a critical probability pc(d). It is believed that critical percolation at and near the critical probability exhibits rich, fractal-like geometry that is expected to be approximately independent of the choice of lattice but highly dependent on the dimension d. In particular, various qualitative distinctions are expected between the low dimensional case d<6, the high-dimensional case d>6, and the critical case d=6, but this remains poorly understood particularly in dimensions d=3,4,5,6.
In this course, I will give an overview of of what is known about critical percolation, focussing on the non-planar models and including a detailed treatment of recent advances in long-range and hierarchical models for which various aspects of intermediate-dimensional critical phenomena can now be understood rigorously.
No prior knowledge of percolation will be assumed.
Speaker: Mathav Murugan
N.B. The microphone was not functioning at the beginning of this session. Audio begins at 28:49
The heat kernel is the fundamental solution to a parabolic partial differential equation. From a probabilistic perspective, the heat kernel is the transition probability density of a stochastic process. Harnack inequalities and functional inequalities such as Poincare and Sobolev inequalities provide tools to understand the relationship between the behavior of the heat kernel and the geometry of the underlying space. An important feature of the approach using functional inequalities is its robustness under perturbations.
The study of the heat kernel and its estimates has produced fruitful interactions between the fields of Analysis, Geometry, and Probability. One of the goals of this course is to illustrate these interactions of heat kernel estimates with functional inequalities, boundary trace processes, quasisymmetric maps, circle packings, the time change of Markov processes, Doob's h-transform, and estimates of harmonic measure or exit distribution.
The setting for this course is a symmetric Markov process which is equivalentlydescribed using a Dirichlet form. This course will contain an introduction to the theory of Dirichlet forms. This theory will be used to construct and analyze Markov processes. This course will survey both classical results and recent progress in our understanding of heat kernel estimates and Harnack inequalities.
Speaker: Nina Holden
Planar maps are graphs embedded in the sphere such that no two edges cross, where we view two planar maps as equivalent if we can get one from the other via a continuous deformation of the sphere. Planar maps are studied in several different branches of mathematics and physics. In particular, in probability theory and theoretical physics random planar maps are used as natural models for discrete random surfaces. In this mini-course we will present scaling limit results for random planar maps and we will focus in particular on a notion of convergence known as convergence under conformal embedding. The limiting surface is a highly fractal surface called a Liouville quantum gravity (LQG) surfaces, which has its origin in string theory and conformal field theory.
Speaker: Mathav Murugan
The heat kernel is the fundamental solution to a parabolic partial differential equation. From a probabilistic perspective, the heat kernel is the transition probability density of a stochastic process. Harnack inequalities and functional inequalities such as Poincare and Sobolev inequalities provide tools to understand the relationship between the behavior of the heat kernel and the geometry of the underlying space. An important feature of the approach using functional inequalities is its robustness under perturbations.
The study of the heat kernel and its estimates has produced fruitful interactions between the fields of Analysis, Geometry, and Probability. One of the goals of this course is to illustrate these interactions of heat kernel estimates with functional inequalities, boundary trace processes, quasisymmetric maps, circle packings, the time change of Markov processes, Doob's h-transform, and estimates of harmonic measure or exit distribution.
The setting for this course is a symmetric Markov process which is equivalentlydescribed using a Dirichlet form. This course will contain an introduction to the theory of Dirichlet forms. This theory will be used to construct and analyze Markov processes. This course will survey both classical results and recent progress in our understanding of heat kernel estimates and Harnack inequalities.
Speaker: Tom Hutchcroft
In Bernoulli bond percolation, we delete or retain each edge of a graph independently at random with some retention parameter p and study the geometry of the connected components (clusters) of the resulting subgraph. For lattices of dimension d>1, percolation has a phase transition, with a infinite cluster emerging at a critical probability pc(d). It is believed that critical percolation at and near the critical probability exhibits rich, fractal-like geometry that is expected to be approximately independent of the choice of lattice but highly dependent on the dimension d. In particular, various qualitative distinctions are expected between the low dimensional case d<6, the high-dimensional case d>6, and the critical case d=6, but this remains poorly understood particularly in dimensions d=3,4,5,6.
In this course, I will give an overview of of what is known about critical percolation, focussing on the non-planar models and including a detailed treatment of recent advances in long-range and hierarchical models for which various aspects of intermediate-dimensional critical phenomena can now be understood rigorously.
No prior knowledge of percolation will be assumed.
Speaker: Nina Holden
Planar maps are graphs embedded in the sphere such that no two edges cross, where we view two planar maps as equivalent if we can get one from the other via a continuous deformation of the sphere. Planar maps are studied in several different branches of mathematics and physics. In particular, in probability theory and theoretical physics random planar maps are used as natural models for discrete random surfaces. In this mini-course we will present scaling limit results for random planar maps and we will focus in particular on a notion of convergence known as convergence under conformal embedding. The limiting surface is a highly fractal surface called a Liouville quantum gravity (LQG) surfaces, which has its origin in string theory and conformal field theory.
Speaker: Tom Hutchcroft
In Bernoulli bond percolation, we delete or retain each edge of a graph independently at random with some retention parameter p and study the geometry of the connected components (clusters) of the resulting subgraph. For lattices of dimension d>1, percolation has a phase transition, with a infinite cluster emerging at a critical probability pc(d). It is believed that critical percolation at and near the critical probability exhibits rich, fractal-like geometry that is expected to be approximately independent of the choice of lattice but highly dependent on the dimension d. In particular, various qualitative distinctions are expected between the low dimensional case d<6, the high-dimensional case d>6, and the critical case d=6, but this remains poorly understood particularly in dimensions d=3,4,5,6.
In this course, I will give an overview of of what is known about critical percolation, focussing on the non-planar models and including a detailed treatment of recent advances in long-range and hierarchical models for which various aspects of intermediate-dimensional critical phenomena can now be understood rigorously.
No prior knowledge of percolation will be assumed.
Speaker: Mathav Murugan
The heat kernel is the fundamental solution to a parabolic partial differential equation. From a probabilistic perspective, the heat kernel is the transition probability density of a stochastic process. Harnack inequalities and functional inequalities such as Poincare and Sobolev inequalities provide tools to understand the relationship between the behavior of the heat kernel and the geometry of the underlying space. An important feature of the approach using functional inequalities is its robustness under perturbations.
The study of the heat kernel and its estimates has produced fruitful interactions between the fields of Analysis, Geometry, and Probability. One of the goals of this course is to illustrate these interactions of heat kernel estimates with functional inequalities, boundary trace processes, quasisymmetric maps, circle packings, the time change of Markov processes, Doob's h-transform, and estimates of harmonic measure or exit distribution.
The setting for this course is a symmetric Markov process which is equivalentlydescribed using a Dirichlet form. This course will contain an introduction to the theory of Dirichlet forms. This theory will be used to construct and analyze Markov processes. This course will survey both classical results and recent progress in our understanding of heat kernel estimates and Harnack inequalities.
Speaker: Mathav Murugan
The heat kernel is the fundamental solution to a parabolic partial differential equation. From a probabilistic perspective, the heat kernel is the transition probability density of a stochastic process. Harnack inequalities and functional inequalities such as Poincare and Sobolev inequalities provide tools to understand the relationship between the behavior of the heat kernel and the geometry of the underlying space. An important feature of the approach using functional inequalities is its robustness under perturbations.
The study of the heat kernel and its estimates has produced fruitful interactions between the fields of Analysis, Geometry, and Probability. One of the goals of this course is to illustrate these interactions of heat kernel estimates with functional inequalities, boundary trace processes, quasisymmetric maps, circle packings, the time change of Markov processes, Doob's h-transform, and estimates of harmonic measure or exit distribution.
The setting for this course is a symmetric Markov process which is equivalentlydescribed using a Dirichlet form. This course will contain an introduction to the theory of Dirichlet forms. This theory will be used to construct and analyze Markov processes. This course will survey both classical results and recent progress in our understanding of heat kernel estimates and Harnack inequalities.
Speaker: Tom Hutchcroft
In Bernoulli bond percolation, we delete or retain each edge of a graph independently at random with some retention parameter p and study the geometry of the connected components (clusters) of the resulting subgraph. For lattices of dimension d>1, percolation has a phase transition, with a infinite cluster emerging at a critical probability pc(d). It is believed that critical percolation at and near the critical probability exhibits rich, fractal-like geometry that is expected to be approximately independent of the choice of lattice but highly dependent on the dimension d. In particular, various qualitative distinctions are expected between the low dimensional case d<6, the high-dimensional case d>6, and the critical case d=6, but this remains poorly understood particularly in dimensions d=3,4,5,6.
In this course, I will give an overview of of what is known about critical percolation, focussing on the non-planar models and including a detailed treatment of recent advances in long-range and hierarchical models for which various aspects of intermediate-dimensional critical phenomena can now be understood rigorously.
No prior knowledge of percolation will be assumed.
Speaker: Tom Hutchcroft
In Bernoulli bond percolation, we delete or retain each edge of a graph independently at random with some retention parameter p and study the geometry of the connected components (clusters) of the resulting subgraph. For lattices of dimension d>1, percolation has a phase transition, with a infinite cluster emerging at a critical probability pc(d). It is believed that critical percolation at and near the critical probability exhibits rich, fractal-like geometry that is expected to be approximately independent of the choice of lattice but highly dependent on the dimension d. In particular, various qualitative distinctions are expected between the low dimensional case d<6, the high-dimensional case d>6, and the critical case d=6, but this remains poorly understood particularly in dimensions d=3,4,5,6.
In this course, I will give an overview of of what is known about critical percolation, focussing on the non-planar models and including a detailed treatment of recent advances in long-range and hierarchical models for which various aspects of intermediate-dimensional critical phenomena can now be understood rigorously.
No prior knowledge of percolation will be assumed.
Speaker: Mathav Murugan
The heat kernel is the fundamental solution to a parabolic partial differential equation. From a probabilistic perspective, the heat kernel is the transition probability density of a stochastic process. Harnack inequalities and functional inequalities such as Poincare and Sobolev inequalities provide tools to understand the relationship between the behavior of the heat kernel and the geometry of the underlying space. An important feature of the approach using functional inequalities is its robustness under perturbations.
The study of the heat kernel and its estimates has produced fruitful interactions between the fields of Analysis, Geometry, and Probability. One of the goals of this course is to illustrate these interactions of heat kernel estimates with functional inequalities, boundary trace processes, quasisymmetric maps, circle packings, the time change of Markov processes, Doob's h-transform, and estimates of harmonic measure or exit distribution.
The setting for this course is a symmetric Markov process which is equivalentlydescribed using a Dirichlet form. This course will contain an introduction to the theory of Dirichlet forms. This theory will be used to construct and analyze Markov processes. This course will survey both classical results and recent progress in our understanding of heat kernel estimates and Harnack inequalities.
Speaker: Kristine Bauer, Luis Seco, Yakine Bahri
This graduation event took place at the end of the 2025 Edition of Math to Power Industry (M2PI). The event begins with an introduction to the M2PI program followed by remarks from invited speakers (Luis Seco, UToronto & Yakine Bhari, BCI).
Speaker: Mathilda Whittle
Concern for the impact of climate change on the spread and severity of infectious disease is widespread. For long-term management of global health, we need to consider parasite evolution under such environmentalchange. Vector-borne diseases are likely to be particularly affected bychanging climates due to the sensitivity of ectothermic vectors to temperature.Here, I present a work-in-progress of an age-structured SI model to represent the ecological dynamics of a general vector-borne disease, incorporating temperature-dependent parameters. Using sequential invasion analyses, the evolutionary trajectory of within-host parasite replication rate, and thus virulence, can then be predicted under a specified heating regime.
Speaker: M. Ram Murty
We will give an exposition on the recent progress in the study of unimodal sequences, beginning with the work of Isaac Newton and then to the contemporary papers of June Huh. We will also relate this topic to the Riemann hypothesis. In the process, we will connect many areas of mathematics ranging from number theory, commutative algebra, algebraic geometry and combinatorics.
Speaker: Chapin Korosec
Following a vaccine inoculation or disease exposure an immune response develops in time, where the description of its time evolution poses an interesting problem in dynamical systems. The principal goal of theoretical immunology is to construct models capable of describing long term immunological trends from the properties and interactions of its elementary components. In this talk I will give a brief description of the human immune system and introduce a simplified version of its elementary components. I will then discuss our contributions to the field achieved through my postdoctoral work with Dr. Jane Heffernan at York University. I will focus on our mechanistic modelling work describing vaccine-generated SARS-CoV-2 immunity and applications of our work towards understanding vaccination responses in people living with HIV. Finally, I will discuss our on-going work towards developing a machine learning public health platform capable of predicting immune response outcomes from repeated-dose immunological data.
Speaker: Octav Cornea
Lagrangian submanifolds are a central object of study in symplectic topology. Their rigidity properties have been uncovered via Floer theory since the early ’90’s. The talk will briefly review the subject, in particular how triangulated category structures naturally arise in this context through work of Donaldson, Kontsevich, Fukaya, and others. Further, will be discussed the more recent, natural role of persistence theory, in the sense common in data science. Finally, we will outline how complexity measurements based on persistence methods reflect topological and dynamical invariants, such as topological entropy.
Speaker: Cameron Smith
TBA
Speaker: Fatemehzahra Janbazi
A classical theorem of Birch and Merriman states that, for fixed 𝑛the set of integral binary 𝑛-ic forms with fixed nonzero discriminant breaks into finitely many GL2(ℤ)-orbits. In this talk, I’ll present several extensions of this finiteness result.
In joint work with Arul Shankar, we study a representation-theoretic generalization to ternary 𝑛-ic forms and prove analogous finiteness theorems for GL3(ℤ)-orbits with fixed nonzero discriminant. We also prove a similar result for a 27-dimensional representation associated with a family of 𝐾3surfaces.
In joint work with Sajadi, we take a geometric perspective and prove a finiteness theorem for Galois-invariant point configurations on arbitrary smooth curves with controlled reduction. This result unifies classical finiteness theorems of Birch–Merriman, Siegel, and Faltings.
Speaker: Arnaud Doucet
Denoising Diffusion models have revolutionized generative modeling. Conceptually, these methods define a transport mechanism from a noise distribution to a data distribution. Recent advancements have extended this framework to define transport maps between arbitrary distributions, significantly expanding the potential for unpaired data translation. However, existing methods often fail to approximate optimal transport maps, which are theoretically known to possess advantageous properties. In this talk, we will show how one can modify current methodologies to compute Schrödinger bridges—an entropy-regularized variant of dynamic optimal transport. We will demonstrate this methodology on a variety of unpaired data translation tasks.
Speaker: Asher Leeks
Viral infections are social processes. Viral replication requires shared gene products that can be used by multiple viral genomes within the same cell, and hence act as public goods. This gives rise to viral cheats, a type of molecular parasite formed by large deletions, that spread by exploiting public goods encoded by full-length viruses. Cheats exist across the viral universe, arise frequently in laboratory infections, and reflect the emergence of evolutionary conflict at the molecular level. In this talk, I will explore two evolutionary consequences of viral cheating that play out at different timescales. Firstly, we will consider the evolution of multipartite viruses, in which the genome is fragmented, and each fragment must separately infect a host. This genome structure comes with clear costs, but has nevertheless evolved multiple times, and today accounts for nearly 40% of known plant viral species. Previous explanations for the evolution of multipartitism have focused on group benefits, but typically require unrealistic rates of coinfection, especially for multipartite viruses with more than two segments. We will argue that cheating provides a contrasting explanation. By combining evolutionary game theory models with agent-based simulations, we will show that the invasion of mutually complementing viral cheats can drive the evolution of multipartitism under far more permissive conditions, including transitions to highly multipartite viruses. This framework shows that multipartitism need not be a group-level adaptation, but can instead emerge as the evolutionary endpoint of the tragedy of the commons. Secondly, we will consider the evolution of cheat-driven extinction in viruses. Cheats emerge spontaneously in laboratory infections of almost all known viruses, driving drastic reductions in viral population sizes. As a result, virologists have long argued that viral infections may be ‘self-limiting’, a claim supported by recent discoveries of cheats in natural viral infections. However, it is unclear whether viral infections provide enough time for viral cheats to emerge, spread, and drive cooperator extinction. Here, we present a birth-death model that incorporates mutation, demographic noise, and a frequency-dependent selective advantage to cheating. We identify qualitatively different dynamical regimes and the timescales under which they lead to viral extinction. We further show that our model can produce characteristic signatures of selection, opening the door to evolutionary biomarkers for predicting the outcome of viral infections from sequencing data. This approach argues that cheating may not only be relevant over long evolutionary timescales, but may also shape viral dynamics in clinically relevant ways, analogous to the emergence of cancer in multicellular organisms.
Speaker: Antonio Pedro Ramos
We consider a variant of a problem first introduced by Hughes and Rudnick (2003) and generalized by Bernard (2015) concerning conditional bounds for small first zeros in a family of L-functions. Here we seek to estimate the size of the smallest intervals centered at a low-lying height for which we can guarantee the existence of a zero in a family of L-functions. This leads us to consider an extremal problem in analysis which we address by applying the framework of de Branges spaces, introduced in this context by Carneiro, Chirre, and Milinovich (2022).
Speaker: Chi Hoi Yip
A set {𝑎1,𝑎2,…,𝑎𝑚}of distinct positive integers is a Diophantine 𝑚-tuple if the product of any two distinct elements in the set is one less than a square. In this talk, I will discuss some recent results related to Diophantine tuples and their generalizations. Joint work with Ernie Croot, Seoyoung Kim, and Semin Yoo.
Speaker: Caroline Mburu
Mathematical modeling, when combined with diverse epidemiological datasets, provides valuable insights for understanding and controlling infectious diseases. In this talk, I will present a series of case studies demonstrating how the synergy between modeling and serological, case-based, and wastewater surveillance data can enhance disease monitoring and inform public health strategies.
Serological data measures biomarkers of infection or vaccination, offering direct estimates of population immunity. This approach complements case data by providing a broader understanding of disease epidemiology. Wastewater surveillance, which detects pathogen genomes in sewage, captures infections across the entire population, including symptomatic, asymptomatic, and pre-/post-symptomatic individuals. This approach complements traditional case reporting by providing a broader, community-wide perspective on disease transmission.
In the first case study, I will discuss how we utilized serological data and a static cohort model to quantify the relative contributions of natural infection, routine vaccination, and supplementary immunization activities (SIAs) to measles seroconversion in Kenyan children. In the second case study we developed a simple static model combined with serological data to evaluate the effectiveness of SIAs in reducing the risk of a measles outbreak in the post-pandemic period. Finally, I will introduce my current work on wastewater-based epidemic modeling for mpox surveillance in British Columbia, demonstrating how wastewater and case data can be integrated within a dynamic transmission model to predict future scenarios of mpox outbreak.
These case studies illustrate the power of mathematical modeling in integrating multiple data sources to inform public health strategies and improve infectious disease control efforts.
Speaker: Wenjun Zhao
This talk will discuss two inference problems in dynamical systems, both motivated by applications in mathematical biology. First, we will discuss the classical gene regulatory network inference problem for time-stamped single-cell datasets and recent advances in optimal transport-based methods for this task. Second, if time permits, I will present an algorithm for bifurcation tracing, which aims to identify interfaces in parameter space. Applications to agent-based models and spatially extended reaction-diffusion equations will be demonstrated, both of which simulate Turing patterns commonly observed in animal skin, vegetation patterns, and more.
Speaker: Antoine Leudière
We will talk about Drinfeld modules, and how they compare to elliptic curves for algorithms and computations.
Drinfeld modules can be seen as function field analogues of elliptic curves. They were introduced in the 1970's by Vladimir Drinfeld, to create an explicit class field theory of function fields. They were instrumental to prove the Langlands program for GL2 of a function field, or the function field analogue of the Riemann hypothesis.
Elliptic curves, to the surprise of many theoretical number theorists, became a fundamental computational tool, especially in the context of cryptography (elliptic curve Diffie-Hellman, isogeny-based post-quantum cryptography) and computer algebra (ECM method).
Despite a rather abstract definition, Drinfeld modules offer a lot of computational advantages over elliptic curves: one can benefit from function field arithmetics, and from objects called Ore polynomials and Anderson motives.
We will use two examples to highlight the practicality of Drinfeld modules computations, and mention some applications.
Speaker: Besfort Shala
I will start with a survey on sums of random multiplicative functions, focusing on distributional questions and almost sure upper bounds and $\Omega$-results. In this context, I will describe previous work with Jake Chinis on a central limit theorem for correlations of Rademacher multiplicative functions, as well as ongoing work on establishing almost sure sharp bounds for them.
Speaker: Andrew Pearce-Crump
It has been known since the 80s, thanks to Conrey and Ghosh, that the average of the square of the Riemann zeta function, summed over the extreme points of zeta up to a height $T$, is $\frac{1}{2} (e^2-5) \log T$ as $T \rightarrow \infty$. This problem and its generalisations are closely linked to evaluating asymptotics of joint moments of the zeta function and its derivatives, and for a time was one of the few cases in which Number Theory could do what Random Matrix Theory could not. RMT then managed to retake the lead in calculating these sorts of problems, but we may now tell the story of how Number Theory is fighting back, and in doing so, describe how to find a full asymptotic expansion for this problem, the first of its kind for any nontrivial joint moment of the Riemann zeta function. This is joint work with Chris Hughes and Solomon Lugmayer.
Speaker: Emily Quesada-Herrera
We will explore how a Fourier optimization framework may be used to study two classical problems in number theory involving Dirichlet characters: The problem of estimating the least character non-residue; and the problem of estimating the least prime in an arithmetic progression. In particular, we show how this Fourier framework leads to subtle, but conceptually interesting, improvements on the best current asymptotic bounds under the Generalized Riemann Hypothesis, given by Lamzouri, Li, and Soundararajan. Based on joint work with Emanuel Carneiro, Micah Milinovich, and Antonio Ramos.
Speaker: Paul Peringuey
Let $\rm{ord}_p(a)$ be the order of $a$ in $( \mathbb{Z} / p \mathbb{Z} )^*$. In 1927, Artin conjectured that the set of primes $p$ for which an integer $a\neq -1,\square$ is a primitive root (i.e. $\rm{ord}_p(a)=p-1$) has a positive asymptotic density among all primes. In 1967 Hooley proved this conjecture assuming the Generalized Riemann Hypothesis (GRH). In this talk we will study the behaviour of $\rm{ord}_p(a)$ as $p$ varies over primes, in particular we will show, under GRH, that the set of primes $p$ for which $\rm{ord}_p(a)$ is “$k$ prime factors away” from $p-1$ has a positive asymptotic density among all primes except for particular values of $a$ and $k$. We will interpret being “$k$ prime factors away” in three different ways, namely $k=\omega(\frac{p-1}{\rm{ord}_p(a)})$, $k=\Omega(\frac{p-1} {\rm{ord}_p(a)})$ and $k=\omega(p-1)-\omega(\rm{ord}_p(a))$, and present conditional results analogous to Hooley's in all three cases and for all integer $k$. From this, we will derive conditionally the expectation for these quantities. Furthermore we will provide partial unconditional answers to some of these questions. This is joint work with Leo Goldmakher and Greg Martin.
Speaker: Alex Mogilner
Individual and collective cell polarity has fascinated mathematical modelers for a long time. Recently, a more subtle type of symmetry breaking started to attract attention of experimentalists and theorists alike - emergence of chirality in single cells and in cell groups. I will describe a joint project with Bershadsky/Tee lab to understand collective cell chirality on adhesive islands. From the initial microscopy data, two potential models emerged: in one, cells elongate and slowly rotate, and neighboring cells align with each other. When the collective rotation is stopped by the island boundaries, chirality emerges. In an alternative model, cells become chiral due to stress fibers turns inside the cells on the boundary, and then the polarity pattern propagates inward into the cellular groups. We used agent-based modeling to simulate these two hypotheses. The models make many predictions, and I will show how we discriminated between the models by comparing the data to these predictions.
Speaker: Arshay Sheth
Even though Euler products of L-functions are generally valid only to the right of the critical strip, there is a strong sense in which they should persist even inside the critical strip. Indeed, the behaviour of Euler products inside the critical strip is very closely related to several major problems in number theory including the Riemann Hypothesis and the Birch and Swinnerton-Dyer conjecture. In this talk, we will give an introduction to this topic and then discuss recent work on establishing asymptotics for partial Euler products of L-functions in the critical strip. We will end by giving applications of these results to questions related to Chebyshev's bias.
Speaker: Lucas Villagra Torcomian
In 1770 Euler observed that $3^3 + 4^3 + 5^3 = 6^3$ and asked if there was another perfect power that equals the sum of consecutive cubes. This captivated the attention of many important mathematicians, such as Cunningham, Catalan, Genocchi and Lucas. In the last decade, the more general equation $x^k + (x+1)^k + \cdots + (x+d)^k = y^n$ began to be studied. In this talk we will focus on this equation. We will see some known results and one of the most used tools to attack this kind of problems. At the end we will show some new results that appear in arXiv:2404.03457.
Speaker: Gilles Mordant
In this talk, we will discuss the question of establishing CLTs for empirical entropic optimal transport when choosing the regularisation parameter as a decreasing function of the sample size. Importantly, decreasing the regularisation parameter enables estimating the population unregularized quantities of interest. Furthermore, we will show an application to score function estimation, a central quantity in diffusion models, and will discuss parallels with recent work on the estimation of transport maps based on the linearization of the Monge—Ampère equation.
Speaker: Matt Olechnowicz
We show that the reduction of a projective endomorphism modulo a discrete valuation naturally takes the form of a set-theoretic correspondence. This raises the possibility of classifying "reduction types" of such dynamical systems, reminiscent of the additive/multiplicative dichotomy for elliptic curves. These correspondences facilitate the exact evaluation of certain integrals of dynamical Green's functions, which arise as local factors in the context of counting rational points ordered by the Call-Silverman canonical height. No prior knowledge of arithmetic dynamics will be assumed.
Speaker: Abbas Maarefparvar
The Polya group of a number field K is a specific subgroup of the ideal class group Cl(K) of K, generated by all classes of Ostrowski ideals of K. In this talk, I will discuss the equality Po(K)=Cl(K) in two directions. First, we will see this equality happens for infinitely many "non-Galois fields'' K. Accordingly, I prove two conjectures presented by Chabert and Halberstadt concerning the Polya groups of some families of non-Galois fields. Then, I present some "finiteness theorems" for the equality Po(K)=Cl(K) for some families of "Galois" fields K obtained in joint work with Amir Akbary (University of Lethbridge).
Speaker: Shubhodip Mondal
In 1966, Tate proposed the Artin–Tate conjectures, which expresses special values of zeta function associated to surfaces over finite fields. Conditional on the Tate conjecture, Milne–Ramachandran formulated and proved similar conjectures for smooth proper schemes over finite fields. The formulation of these conjectures already relied on other unproven conjectures. In this talk, I will discuss an unconditional formulation and proof of these conjectures.
Speaker: Dmitry Frolenkov
I am going to discuss various results on moments of symmetric square L-functions and some of their applications. I will mainly focus on a recent result of R. Khan and M. Young and our improvement of it. Khan and Young proved a mean Lindelöf estimate for the second moment of Maass form symmetric-square L-functions $L(\mathop{sym}^2 u_j, 1/2 + it)$ on the short interval of length $G >> |t_j|^{(1 + \epsilon)/t^{(2/3)}}$, where $t_j$ is a spectral parameter of the corresponding Maass form. Their estimate yields a subconvexity estimate for $L(\mathop{sym}^2 u_j, 1/2 + it)$ as long as $|t_j|^{(6/7 + \delta)} << t < (2 - \delta)|t_j|$. We obtain a mean Lindelöf estimate for the same moment in shorter intervals, namely for $G >> |t_j|^{(1 + \epsilon)/t}$. As a corollary, we prove a subconvexity estimate for $L(\mathop{sym}^2 u_j, 1/2 + it)$ on the interval $|t_j|^{(2/3 + \delta)} << t << |t_j|^{(6/7 - \delta)}$. This is joint work with Olga Balkanova.
Speaker: Abbas Maarefparvar
The Polya group P o ( K ) of a Galois number field K coincides with the subgroup of the ideal class group C l ( K ) of K consisting of all strongly ambiguous ideal classes. We prove that there are only finitely many imaginary abelian number fields K whose "Polya index" [ C l ( K ) : P o ( K ) ] is a fixed integer. Accordingly, under GRH, we completely classify all imaginary quadratic fields with the Polya indices 1 and 2. Also, we unconditionally classify all imaginary biquadratic and imaginary tri-quadratic fields with the Polya index 1. In another direction, we classify all real quadratic fields K of extended R-D type (with possibly only one more field K ) for which P o ( K ) = C l ( K ) . Our result generalizes Kazuhiro's classification of all real quadratic fields of narrow R-D type whose narrow genus numbers are equal to their narrow class numbers.
This is a joint work with Amir Akbary (University of Lethbridge).
Speaker: Kim Klinger-Logan
Previously we found certain convolution sums of divisor functions arising from physics yield Fourier coefficients of modular forms. In this talk we will discuss the limitations of the current proof of these formulas. We will also explore the connection with the Petersson and Kuznetsov Trace Formulae and the possibility of extending these formulas to other cases. The work mentioned in this talk is in collaboration with Ksenia Fedosova, Stephen D. Miller, Danylo Radchenko, and Don Zagier.
Speaker: Amie Wilkinson
I will discuss a result with Bonatti and Crovisier from 2009 showing that the C^1 generic diffeomorphism f of a closed manifold has trivial centralizer; i.e. fg = gf implies that g is a power of f. I’ll discuss features of the C^1 topology that enable our proof (the analogous statement is open in general in the C^r topology, for r>1). I’ll also discuss some features of the proof and some recent work, joint with Danijela Damjanovic and Disheng Xu that attempts to tackle the non-generic case.
Speaker: Yunan Yang
Measures provide valuable insights into long-term and global behaviors across a broad range of dynamical systems. In this talk, we present our recent research efforts that employ measure theory and optimal transport to tackle core challenges in system identification, parameter recovery, and predictive modeling. First, we adopt a PDE-constrained optimization perspective to learn ODEs and SDEs from slowly sampled trajectories, enabling stable forward models and uncertainty quantification. We then use optimal transportation to align physical measures for parameter estimation, even when time-derivative data is unavailable. Our second result extends the celebrated Takens’ time-delay embedding, a foundational result in dynamical systems, from state space to probability distributions. It establishes a robust theoretical and computational framework for state reconstruction that remains effective under noisy and partial observations. Finally, we show that by comparing invariant measures in time-delay coordinates, one can overcome identifiability challenges and achieve unique recovery of the underlying dynamics even though it is not generally possible to uniquely reconstruct dynamics using invariant statistics alone. Collectively, these works demonstrate how measure-theoretic and transport-based methods can robustly identify, analyze, and forecast real-world dynamical systems and the great research potential of measure-theoretic approaches for dynamical systems.
Speaker: Gregg Knapp
Let $d>k$ be positive integers. Motivated by an earlier result of Bugeaud and Nguyen, we let $E_{k,d}$ be the set of $(c_1,\ldots,c_k)\in\mathbb{R}_{\geq 0}^k$ such that $\vert\alpha_0\vert\vert\alpha_1\vert^{c_1}\cdots\vert\alpha_k\vert^{c_k}\geq 1$ for any algebraic integer $\alpha$ of degree $d$, where we label its Galois conjugates as $\alpha_0,\ldots,\alpha_{d-1}$ with $\vert\alpha_0\vert\geq \vert\alpha_1\vert\geq\cdots \geq \vert\alpha_{d-1}\vert$. First, we give an explicit description of $E_{k,d}$ as a polytope with $2^k$ vertices. Then we prove that for $d>3k$, for every $(c_1,\ldots,c_k)\in E_{k,d}$ and for every $\alpha$ that is not a root of unity, the strict inequality $\vert\alpha_0\vert\vert\alpha_1\vert^{c_1}\cdots\vert\alpha_k\vert^{c_k}>1$ holds. We also provide a quantitative version of this inequality in terms of $d$ and the height of the minimal polynomial of $\alpha$.
Speaker: Alexandre de Faveri
I will discuss recent work with Chantal David, Alexander Dunn, and Joshua Stucky, in which we prove that a positive proportion of Hecke L-functions associated to the cubic residue symbol modulo square-free Eisenstein integers do not vanish at the central point. Our principal new contribution is the asymptotic evaluation of the mollified second moment. No such asymptotic formula was previously known for a cubic family (even over function fields).
Our new approach makes crucial use of Patterson's evaluation of the Fourier coefficients of the cubic metaplectic theta function, Heath-Brown's cubic large sieve, and a Lindelöf-on-average upper bound for the second moment of cubic Dirichlet series that we establish. The significance of our result is that the family considered does not satisfy a perfectly orthogonal large sieve bound. This is quite unlike other families of Dirichlet L-functions for which unconditional results are known (namely the family of quadratic characters and the family of all Dirichlet characters modulo q). Consequently, our proof has fundamentally different features from the corresponding works of Soundararajan and of Iwaniec and Sarnak.