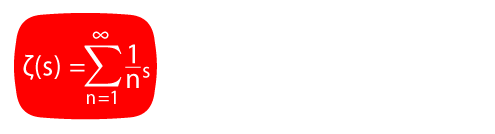Moments of symmetric square L-functions

I am going to discuss various results on moments of symmetric square L-functions and some of their applications. I will mainly focus on a recent result of R. Khan and M. Young and our improvement of it. Khan and Young proved a mean Lindelöf estimate for the second moment of Maass form symmetric-square L-functions $L(\mathop{sym}^2 u_j, 1/2 + it)$ on the short interval of length $G >> |t_j|^{(1 + \epsilon)/t^{(2/3)}}$, where $t_j$ is a spectral parameter of the corresponding Maass form. Their estimate yields a subconvexity estimate for $L(\mathop{sym}^2 u_j, 1/2 + it)$ as long as $|t_j|^{(6/7 + \delta)} << t < (2 - \delta)|t_j|$. We obtain a mean Lindelöf estimate for the same moment in shorter intervals, namely for $G >> |t_j|^{(1 + \epsilon)/t}$. As a corollary, we prove a subconvexity estimate for $L(\mathop{sym}^2 u_j, 1/2 + it)$ on the interval $|t_j|^{(2/3 + \delta)} << t << |t_j|^{(6/7 - \delta)}$. This is joint work with Olga Balkanova.