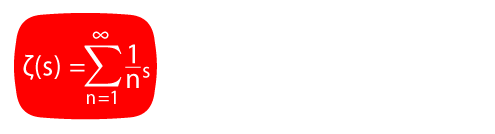Fourier optimization and the least quadratic non-residue

We will explore how a Fourier optimization framework may be used to study two classical problems in number theory involving Dirichlet characters: The problem of estimating the least character non-residue; and the problem of estimating the least prime in an arithmetic progression. In particular, we show how this Fourier framework leads to subtle, but conceptually interesting, improvements on the best current asymptotic bounds under the Generalized Riemann Hypothesis, given by Lamzouri, Li, and Soundararajan. Based on joint work with Emanuel Carneiro, Micah Milinovich, and Antonio Ramos.