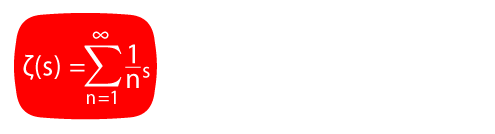Periods and Quantization

A number is called a "period" if it can be expressed as the volume of a region in Euclidean space, defined by polynomial inequalities with rational coefficients. Many famous constants, such as π, log(2) and special values of the Riemann zeta function, are periods. Consequently, periods play an important role in many parts of mathematics and science. For example, they arise naturally when relating the mathematics of classical and quantum mechanics (Poisson geometry and noncommutative algebra, respectively), via a procedure known as "deformation quantization". It turns out that algebraic geometry endows periods with a wealth of rich and surprising structure, such as a "motivic Galois group" of symmetries, which constrains their properties and facilitates their calculation. I will give an introduction to this circle of ideas, emphasizing their role in recent developments in deformation quantization.